Degraders in MOCADI
H. Weick 14.Jan 2011
There are two kind of degraders implemented in MOCADI trapezoidal
shape
and curved sheet.
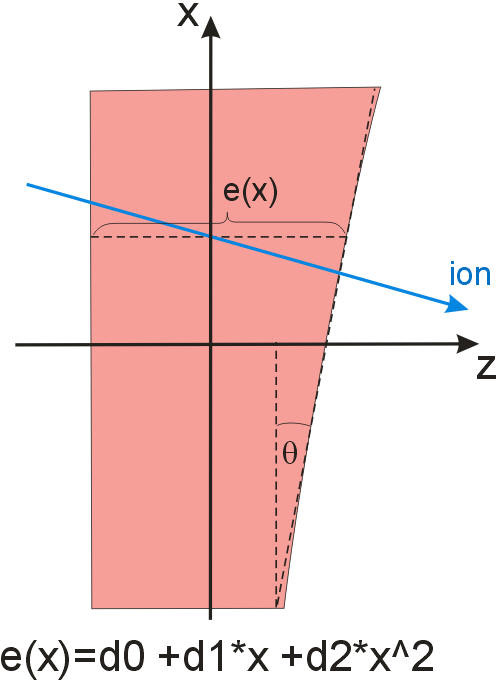
1.) Trapezoidal shape
The required thickness variation in z direction as function of transverse
position x is realized by shaping one side of the degrader. A polynomial up to
second order can be used to describe the thickness e(x). e(x) can be entered in
units of cm or mg/cm2. The coefficient for slope d_1 then has units of 1 or
mg/cm^3, the one for 2nd order 1/cm or mg/cm^4. The wedge angle (q)
can be derived directly from the slope of the edge, tan(q) = d_1 [mg/cm^3] /
density [mg/cm^3]. Note, the definition of the sign of q
is opposite to the definition in LISE++.
The center of the degrader for x=0
corresponds to the optical plane where the WEDGE command was entered.
All effects of the wedge are compressed to an element of zero length in the
optical plane. Angular scattering inside the matter can therefore lead to small
jumps of trajectory at z=0.
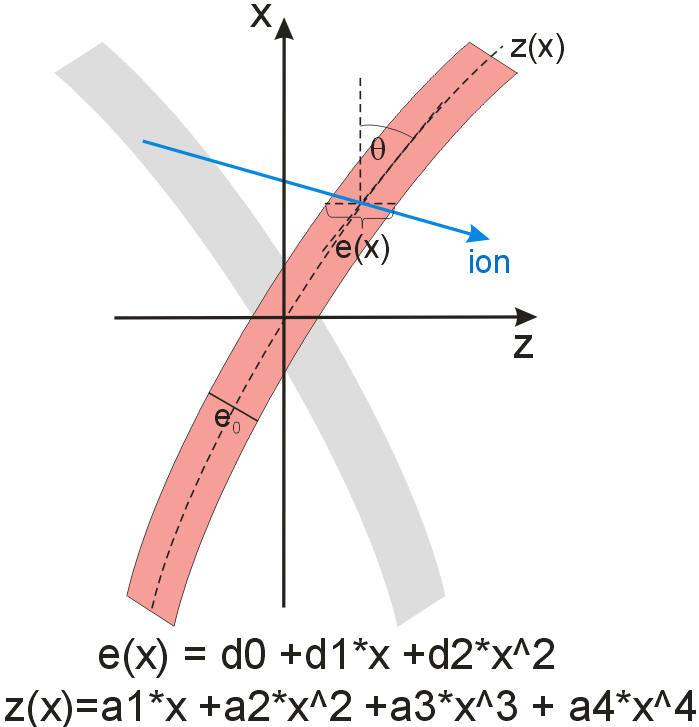
2.) Curved sheet
The required thickness variation in z direction as
function of transverse position x is realized by the different curvature and the
corresponding longer path length in matter. MOCADI uses an approximate solution
of the integral to convert the polynomial for the thickness variation e(x) into
a polynomial z(x) for the curve. This is based on a Taylor expansion of z(x) up
to fourth order. In this case the tilt of the curve q
at a position x does not correspond to the wedge angle.
The input can be made either by giving e(x) like for a trapezoidal
wedge [in units of cm or mg/cm^2] or by entering z(x) [in cm]. Both solutions
bending the sheet in forward or backward direction will satisfy the desired
thickness variation, see red and grey sheet in graph. The direction can be chosen by different input for i_mode.
The curve z(x) always goes through the optical plane of input at x=0. MOCADI
computes the entrance and exit position to the wedge of a given thickness e0,
which is required as additional input in case of a curved sheet. From this
follows the thickness in direction of the ion.
Due to the strong tilt and curvature ions are slowed down earlier and later,
this causes a larger difference in time-of-flight. As the the effect of the wedge is
compressed to zero length in the optical plane the time can also be negative.
For trajectory calculations all angular scattering is assumed to happen at the
exit of the degrader, changes of the trajectory due to angular scattering inside
the degrader are not considered yet.