deflection function J₁(b) at relativistic energies:

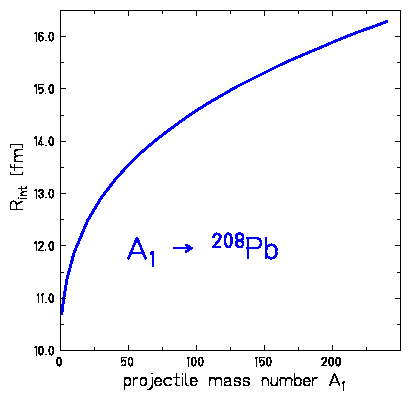
where T_lab is the laboratory energy in MeV, A₁,Z₁ and A₂,Z₂ are the mass (in amu) and charge number of the projectile and target nucleus and the impact parameter b (in fm). For bombarding energies larger than 100 MeV/u, the impact parameter b becomes identical with the distance of closest approach D. In case of electromagnetic interaction the smallest distance of closest approach is the nuclear interaction radius R_int which can be estimated using the following formulae (At.Data Nucl.Data Tables 25 (1980),389).

Figure 1: The nuclear interaction radius R_int is displayed as a function of projectile mass number A₁, if a ²⁰⁸Pb target is assumed.

nuclear radius for homogeneous (sharp) mass distribution:

nuclear radius for diffuse (Fermi) mass distribution:

nuclear interaction radius:

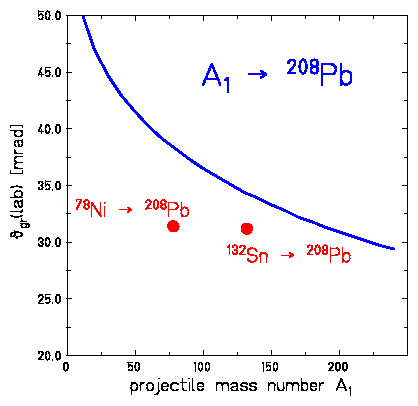
For the nuclear interaction radius R_int the grazing angle J_gr(lab) can be calculated using the following formula.

grazing angle:

Figure 2: The grazing angle J_gr(lab) is displayed as a function of projectile mass number A₁, if a ²⁰⁸Pb target is assumed. The blue line corresponds to the nuclei in the valley of stability