![]()
Figure: For each projectile the trajectory is
measured by two position-sensitive parallel plate counters
(PPAC-1 and PPAC-2). For a straight line trajectory the
interaction point at the target and the expected position
at PPAC-3 can be calculated. This information allows the
orientation of a coordinate system along the trajectory
with its origion in the interaction point at the target.
From the measured position (PPAC-3) of the projectile and
the constructed coordinate system one can determine the
scattering angle.
straight line equation:
![]()
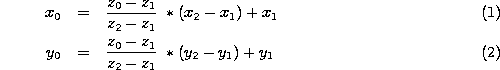
and
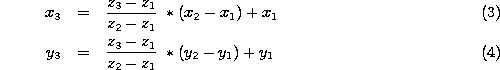
Origin ![]() of a new coordinate system
of a new coordinate system
Transformation of coordinate system

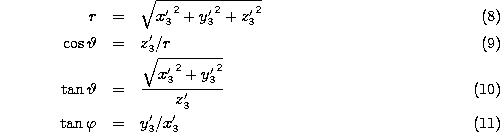
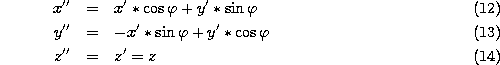
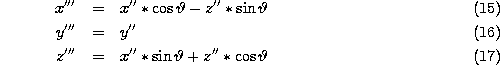
The z'''-axis of the shifted and rotated coordinate system coincides with the straight-line trajectory calculated from the position of PPAC-1 and PPAC-2.
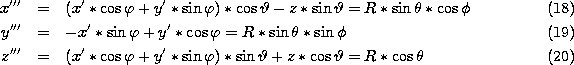
with ![]() .
For the calculated position
.
For the calculated position ![]() one
obtains a scattering angle (
one
obtains a scattering angle ( ![]() ,
, ![]() )=(
)=( ![]() ).
).
The measured position ![]() transformed to the shifted
and rotated coordinate system
transformed to the shifted
and rotated coordinate system ![]() yields the scattering angle (
yields the scattering angle ( ![]() ,
, ![]() ).
).
As a result of this transformation
the angles ( ![]() ) of each
) of each ![]() -detector
have also to be calculated from the fixed position
-detector
have also to be calculated from the fixed position ![]() for each projectile.
for each projectile.
![]()
![]()
![]()
![]()
1. step: expected position at target ( ![]() ) and PPAC-3 (
) and PPAC-3 ( ![]() )
)
![]()
![]()
2. step: spherical coordinates for ![]()
![]()
![]()
3. step: rotation of the coordinate system around z'-axis
![]()
4. step: rotation of the coordinate system around y''-axis
![]()
For the calculated position ![]() the scattering angle would be
the scattering angle would be ![]() and
and ![]() .
.
measured position of scattered projectile ( ![]() ):
):
![]()
result: r=200.73, ![]() ,
, ![]() .
.
position of Ge-detector ( ![]() ):
):
![]()
result: r=99.84, ![]() ,
, ![]() .
.