-Ray Angular Correlation of Fission Fragments
The angular momentum distribution in the primary fission fragments
provides information on the properties of the fissioning nucleus
from the time it goes through the saddle point until shortly after
scission. The angular momentum distribution of the fragments, in
particular, bears a close relationship to vibrations of matter in the
neck normal to the fission direction [1]. At scission this
results in angular momentum of the fragments normal to their axis
of separation; thus angular momentum is induced even in fragments
from spontaneously fissioning nuclei such as 
, which
originally have spin zero. Coulomb excitation between the separating
fragments can also alter the angular momentum distribution present
at scission. Since the characteristics of the -ray deexcitation
of the fragments are particularly sensitive to the magnitude and
orientation of the angular momentum of the fragments, studies of
-ray emission from fission have provided most of the knowledge
about the angular momentum in fission.
Most of the energy released in fission is converted into translational kinetic energy of the fragments. The remaining excitation energy, which is too low to have a reasonable probability for charged particle emission, will be distributed among neutrons and gammas. Neutron emission is not expected to decrease the spin of the fragments by more than one unit of angular momentum and is as such of less importance in the determination of the initial fragment spins. Gamma emission, on the contrary, is a very suitable tool in studying initial fragment spins because the emission time, the number, the energy, and the multipolarity of the gammas strongly depend on the value of the primary angular momentum.
Figure 1: A schematic illustration of the alignment of fragment
spins perpendicular to the fission axis.
Spin vectors of fission fragments are mainly oriented perpendicular
to the fission direction (i.e. aligned), in accordance both with
collective vibrational motion at scission (so-called bending or
wriggling modes) and with postscission Coulomb excitation. This
alignment of fragment spins causes the emission of the yrast
-rays to proceed anisotropically with respect to the fission
axis.
Calculation of the -Ray Angular Correlation
If one assumes that only the magnetic substate with m=0 is populated
(complete alignment) and no feeding from higher-lying states is considered,
the -ray angular correlation for a
strechted E2 transition ( 
is given by
with
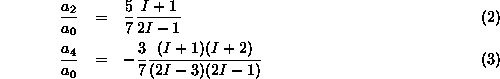
The Legendre polynomials are given by
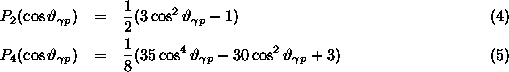
with
define the direction of the
-ray in the laboratory system. The excited fission fragment
is measured at laboratory angles 
.
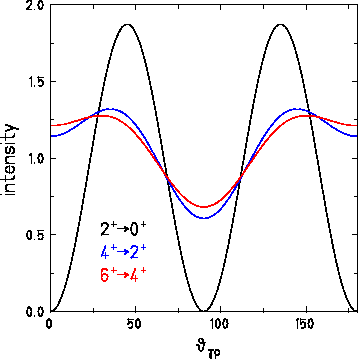
Figure 2: -ray angular correlation for the
, 
, 
transition as a function of 
.
The Experiment
Doppler-shift corrected -ray spectra
The experimental setup comprises a double ionization chamber, the GSI
Clover detector and a thin spontaneous fission source
(1000 fissions/s) that allows the fission fragments to leave the source.
In a coincidence measurement the kinetic energies of the two fission
products were measured simultaneously with single -rays. The
masses of the fission fragments were determined from the measured
kinetic energies. The emission angle ( ) of the fragments
were determined from the drift-time of the anode and the energy signal
of the cathode sections, respectively.
The fission fragments leave the source with velocities on the order of
a few percent of the speed of light (e.g. 
for the Ba-isotopes).
The measured energies of the -rays emitted during the flight
of the fission fragments are appreciably Doppler shifted and need to
be transformed back to their rest frame to extract the transition energies.
The transformation of the -energies to their rest frame is
given by
where 
is the true transition energy in the de-exciting
nuclei's rest frame, 
is the energy measured in the lab
frame, is the angle between the fission
fragment velocity vector and the direction of the emitted -ray
in the lab frame, and 
. The velocities of the fission
fragments are determined from the measured kinetic energies. The angle
between the emitted -ray and the direction of the moving nuclei,
, is known since the orientation of the fission axis
( ) is measured, and the direction of the
-ray ( ) is measured by
16 segments of the GSI Clover detector. The angle
is given by
where and
are the direction of travel of the nuclei and -ray, respectively.
One has to use the positive sign if the excited fragment moves into the
direction of the GSI Clover detector, and the negative sign for the
opposite direction. The polar angle 
is always given in a
range between 
and 
.
Two spectra after Doppler correction are shown in Fig. 3. Sharp -ray
line shapes are recovered by performing the Doppler correction on an
event-by event basis. It is not known a priori whether a detected
-ray was emitted from the heavy or light fission partner and,
hence, it is not determined whether Doppler correction should be performed
for the heavy or light nucleus. In the present example, the Doppler
correction of the heavy fragment was applied to the data set. Sharp
-ray line shapes are recovered for the heavy nuclei's -rays,
and the light nuclei's -ray line shapes are broadened further.
Figure 3: The figure shows mass-gated and Doppler-corrected
-ray spectra. In the top spectrum the ,
transition of 
at 483 keV is indicated,
while the of 
at 331 keV is
marked in the bottom spectrum.
Mass Measurement
The average value of the total kinetic energy released for a given
mass division ( 
), and its standard deviation
, in spontaneous fission of are
well measured quantities [2, 3, 4, 5]. The
can be used to calculate the initial recoil energies
of the emitted fission fragment pairs. With the inclusion of
experimental conditions, such as energy loss of the recoiling fission
fragments in the source material, the experimentally measured anode
energies can be used to deduce the fission masses on an event-by-event
basis.
The resolution of the mass measurement based on the kinetic energies
of the fission fragments is about 6-7 mass units (FWHM). The resolution
was measured by gating the -ray spectra on transitions in
specific nuclei and projecting the measured mass for these events.
An example of the mass measurement is shown in Fig. 4.
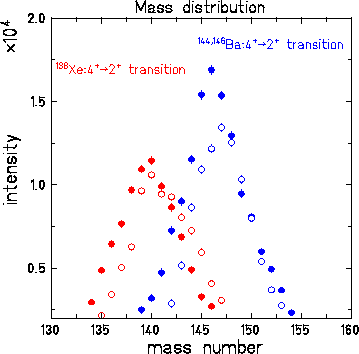
Figure 4: Measured mass resolution. The measured mass for individual
nuclei are projected by setting a single gate on known -ray transitions.
For the , transition of
at 483 keV (red) and the of
at 331 keV (blue) the mass distribution are displayed. The full symbols
are measured with the ionization chamber facing the source side, while
the open symbols are data from the backing side of the source.
For the -ray angular distribution study the intensities of individual
-rays were measured relative to the fission fragment axis. Prompt
fission -rays were recorded for 16 segments of the GSI Clover
detector (distance from the source: 11.4 cm) in coincidence
with the fragment masses which have been measured for three different
polar angular regions ( 
, 
, 
) and
four azimuthal angular region ( 
with
). For the present experimental setup the
intensities of -ray transitions were determined at 36 different
angles in one experimental run. This number is considerably smaller than
the expected value of 192, which results from the symmetric position
of the GSI Clover detector relative to the double ionization chamber.
On the other hand it increases the statistics in the remaining spectra.
Angular distribution results are shown in Fig. 5.
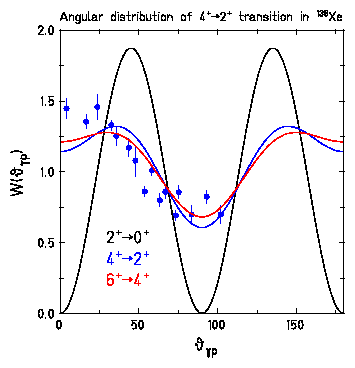
Figure 5: Angular distribution of the transitions
of at 331 keV relative to the fission axis. The line represents
a calculated angular correlation if one assumes that only the magnetic
with m=0 is populated (complete alignment).