-Ray Transitions
In prolate, axially symmetric nuclei the projection of the angular
momentum I onto the nuclear symmetry axis, K, is an approximately
good quantum number. For a collective rotation the nucleus rotates
around an axis perpendicular to the symmetry 3-axis which results
in a projection of the angular momentum of K=0 for the ground state
band. If one breaks a pair of nucleons near the Fermi surface,
the single-particle angular momenta ( 
) may align parallel
to the deformation 3-axis leading to high K-values
( 
, where 
is the projection
of the single-particle angular momentum 
).
In this case the nucleus seems to rotate around the prolate
symmetry 3-axis. Both coupling schemes are sketched in fig.1.
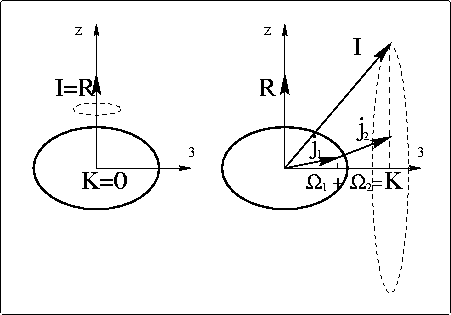
Figure 1: Schematic diagrams illustrating the collective rotation of an
even-even nucleus (left) and the coupling scheme of two individual nucleons with
the collective rotation of the core (right).
Transitions between the two classes of quantum states are governed by
the K-selection rule. If the difference in K-quantum number
is larger than the multipole order L,
electromagnetic transitions are forbidden. The observation
of 'forbidden' transitions establishes the generally important role
of K-mixing. Some admixture may be associated with (i) interplay
between intrinsic (particle) motion and rotational motion
(e.g. Coriolis interaction) and (ii) deviations from axial symmetry.
As a consequence of this, the multi-quasi-particle states with high
K-values are often isomeric. For K-forbidden transitions it is
sometimes useful to compare experimental transition probabilities
to the Weisskopf estimate for different values.
The systematic nature of the inhibitions was first illustrated by
Loebner [Loe68a, Loe68b], who demonstrated the clear correlation of the
Weisskopf hindrance factor 
, with the degree of K-forbiddenness,
(see fig.2). The hindrance factor is
defined by the ratio of experimental -ray transition probabilities
to the Weisskopf estimate.
where 
is the partial -ray half-life and
is the reduced transition probability for eletric (E) or
magnetic (M) multipolarity L. The partial -ray half-life is
obtained from the mean lifetime 
or the half-life
where the sum over k has to include all levels into which the level
N can decay and the sum over L includes all multipoles in
the transition 
. The partial -ray transition
probability 
is defined by
For a simple case, e.g. a single depopulating -ray transition with
E1 multipolarity, the relation between the partial -ray half-life
and the total -ray half-life of the level can be given as a
function of the total internal conversion coefficient 
:
However, for the general case of several depopulating transitions of mixed multipolarity such formula becomes more complicated.
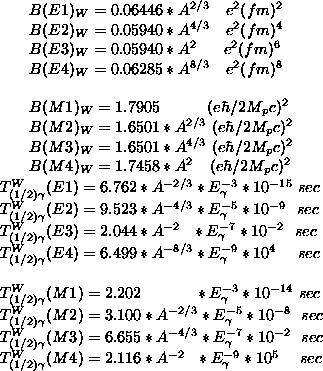
Table 2: Partial -ray half-lives according to the Weisskopf
estimate for different multipole transitions using a nuclear radius
of 
(A=mass number and 
=transition energy in MeV).
Table 1: Numerical values of the reduced Weisskopf single-particle
transition probabilities using a nuclear radius of .
The reduced transition probabilities and the partial -ray
half-lives according to the Weisskopf estimate for different multipolarities
are presented in table 1 and in table 2, respectively.
The partial -ray half-lives according to the Weisskopf
estimate (Table 2) are used to obtain the hindrance factor
which is calculated in the following for a particular case.
In 
Hf, two unpaired nucleons couple their angular momentum
to a total angular momentum 
.
This excited state with a level energy of 
and a half-life 
decays
via a 88.9 keV -ray with multipolarity E1 ( 
)
to the 
-level ( 
) of the ground state band
(K=0). The partial -ray half-life according to the Weisskopf
estimate is 
which can be
related to the measured -ray half-life
leading to a
Weisskopf hindrance factor 
.
The dependence on of the hindrance factor
for -rays with E1 multipolarities can be seen from fig.2
(above the broken line for K-allowed and below for K-forbidden
transitions).
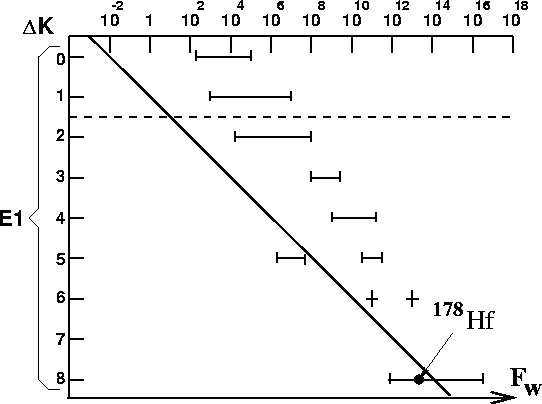
Figure 2: Range of hindrance factors relative to the Weisskopf
estimate of E1 -ray transitions for different
values (for explanation see text).
The solid line shows the dependence of on
according to the 'empirical rule' proposed by Rusinov [Rus61]:
Although the indrance factors scatter considerably the following
conclusions can be drawn from this figure:
(1) The -values increase approximately by a factor of 100 per
degree of K-forbiddenness 
. However, the
frequently used empirical rule of Rusinov is not generally true,
since the -values of K-allowed -ray transitions do not
show hindrance factors near unity.
(2) The increase of the hindrance for each degree of K-forbiddenness
shows that mixing of states which differ by large values of
is small. This suggests that K is in most cases
approximately a good quantum number. From this one can conclude
that most of the strong deformed nuclei have to a first approximation
an axially symmetric equilibrium shape. For large deviations
from axial symmetry K would not even approximately be a good
quantum number.
