Computes the associated Legendre polynomials.
![\[ P_{l}^{m}(x) = (1-x^2)^{m/2} \frac{d^m}{dx^m} P_{l}(x) \]](form_117.png)
with 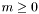 ,
, 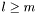 and
and 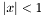 . There are two sign conventions for associated Legendre polynomials. As is the case with the above formula, some authors (e.g., Arfken 1985, pp. 668-669) omit the Condon-Shortley phase
. There are two sign conventions for associated Legendre polynomials. As is the case with the above formula, some authors (e.g., Arfken 1985, pp. 668-669) omit the Condon-Shortley phase 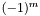 , while others include it (e.g., Abramowitz and Stegun 1972). One possible way to distinguish the two conventions is due to Abramowitz and Stegun (1972, p. 332), who use the notation
, while others include it (e.g., Abramowitz and Stegun 1972). One possible way to distinguish the two conventions is due to Abramowitz and Stegun (1972, p. 332), who use the notation
![\[ P_{lm} (x) = (-1)^m P_{l}^{m} (x)\]](form_122.png)
to distinguish the two. For detailed description see Mathworld. The implementation used is that of GSL.
The definition uses is the one of C++0x, 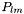 , while GSL and MatheMatica use the
, while GSL and MatheMatica use the 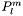 definition. Note that C++0x and GSL definitions agree instead for the normalized associated Legendre polynomial, sph_legendre(l,m,theta).
definition. Note that C++0x and GSL definitions agree instead for the normalized associated Legendre polynomial, sph_legendre(l,m,theta).
Definition at line 52 of file SpecFuncMathMore.cxx.
Referenced by RooLegendre::evaluate(), G__G__MathMore_99_0_5(), G__setup_memfuncROOTcLcLMath(), RooMathMoreReg::RooMathMoreReg(), and testSpecFunc().
![\[ Ai(x) = \frac{1}{\pi} \int\limits_{0}^{\infty} \cos(xt + t^3/3) dt \]](form_151.png)
![\[ Bi(x) = \frac{1}{\pi} \int\limits_{0}^{\infty} [\exp(xt-t^3/3) + \cos(xt + t^3/3)] dt \]](form_152.png)
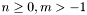 . They are defined in terms of the confluent hypergeometric function. For integer values of m they can be defined in terms of the Laguerre polynomials
. They are defined in terms of the confluent hypergeometric function. For integer values of m they can be defined in terms of the Laguerre polynomials 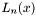 :
:![\[ L_{n}^{m}(x) = (-1)^{m} \frac{d^m}{dx^m} L_{n+m}(x) \]](form_116.png)
![\[ P_{l}^{m}(x) = (1-x^2)^{m/2} \frac{d^m}{dx^m} P_{l}(x) \]](form_117.png)
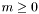 ,
, 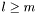 and
and 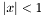 . There are two sign conventions for associated Legendre polynomials. As is the case with the above formula, some authors (
. There are two sign conventions for associated Legendre polynomials. As is the case with the above formula, some authors (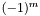 , while others include it (
, while others include it (![\[ P_{lm} (x) = (-1)^m P_{l}^{m} (x)\]](form_122.png)
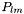 , while GSL and MatheMatica use the
, while GSL and MatheMatica use the 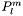 definition. Note that C++0x and GSL definitions agree instead for the normalized associated Legendre polynomial, sph_legendre(l,m,theta).
definition. Note that C++0x and GSL definitions agree instead for the normalized associated Legendre polynomial, sph_legendre(l,m,theta).
![\[ B(x,y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} \]](form_110.png)
![\[ K(k) = F(k, \pi / 2) = \int_{0}^{\pi /2} \frac{d \theta}{\sqrt{1 - k^2 \sin^2{\theta}}} \]](form_125.png)
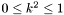 . For detailed description see
. For detailed description see ![\[ E(k) = E(k , \pi / 2) = \int_{0}^{\pi /2} \sqrt{1 - k^2 \sin^2{\theta}} d \theta \]](form_127.png)
![\[ \Pi (n, k, \pi / 2) = \int_{0}^{\pi /2} \frac{d \theta}{(1 - n \sin^2{\theta})\sqrt{1 - k^2 \sin^2{\theta}}} \]](form_128.png)
![\[ _{1}F_{1}(a;b;z) = \frac{\Gamma(b)}{\Gamma(a)} \sum_{n=0}^{\infty} \frac{\Gamma(a+n)}{\Gamma(b+n)} \frac{z^n}{n!} \]](form_129.png)
![\[ U(a,b,z) = \frac{ \pi}{ \sin{\pi b } } \left[ \frac{ _{1}F_{1}(a,b,z) } {\Gamma(a-b+1) } - \frac{ z^{1-b} { _{1}F_{1}}(a-b+1,2-b,z)}{\Gamma(a)} \right] \]](form_130.png)
![\[ Ci(x) = - \int_{x}^{\infty} \frac{\cos t}{t} dt = \gamma + \ln x + \int_{0}^{x} \frac{\cos t - 1}{t} dt\]](form_113.png)
![\[ I_{\nu} (x) = i^{-\nu} J_{\nu}(ix) = \sum_{k=0}^{\infty} \frac{(\frac{1}{2}x)^{\nu + 2k}}{k! \Gamma(\nu + k + 1)} \]](form_131.png)
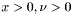 . For detailed description see
. For detailed description see ![\[ J_{\nu} (x) = \sum_{k=0}^{\infty} \frac{(-1)^k(\frac{1}{2}x)^{\nu + 2k}}{k! \Gamma(\nu + k + 1)} \]](form_133.png)
![\[ K_{\nu} (x) = \frac{\pi}{2} i^{\nu + 1} (J_{\nu} (ix) + iN(ix)) = \left\{ \begin{array}{cl} \frac{\pi}{2} \frac{I_{-\nu}(x) - I_{\nu}(x)}{\sin{\nu \pi}} & \mbox{for non-integral $\nu$} \\ \frac{\pi}{2} \lim{\mu \to \nu} \frac{I_{-\mu}(x) - I_{\mu}(x)}{\sin{\mu \pi}} & \mbox{for integral $\nu$} \end{array} \right. \]](form_134.png)
![\[ N_{\nu} (x) = Y_{\nu} (x) = \left\{ \begin{array}{cl} \frac{J_{\nu} \cos{\nu \pi}-J_{-\nu}(x)}{\sin{\nu \pi}} & \mbox{for non-integral $\nu$} \\ \lim{\mu \to \nu} \frac{J_{\mu} \cos{\mu \pi}-J_{-\mu}(x)}{\sin{\mu \pi}} & \mbox{for integral $\nu$} \end{array} \right. \]](form_135.png)
![\[ F(k, \phi) = \int_{0}^{\phi} \frac{d \theta}{\sqrt{1 - k^2 \sin^2{\theta}}} \]](form_136.png)
![\[ E(k , \phi) = \int_{0}^{\phi} \sqrt{1 - k^2 \sin^2{\theta}} d \theta \]](form_137.png)
![\[ \Pi (n, k, \phi) = \int_{0}^{\phi} \frac{d \theta}{(1 - n \sin^2{\theta})\sqrt{1 - k^2 \sin^2{\theta}}} \]](form_138.png)
![\[ erf(x) = \frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-t^2} dt \]](form_105.png)
![\[ erfc(x) = 1 - erf(x) = \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} e^{-t^2} dt \]](form_106.png)
![\[ Ei(x) = - \int_{-x}^{\infty} \frac{e^{-t}}{t} dt \]](form_139.png)
![\[ _{2}F_{1}(a,b;c;x) = \frac{\Gamma(c)}{\Gamma(a) \Gamma(b)} \sum_{n=0}^{\infty} \frac{\Gamma(a+n)\Gamma(b+n)}{\Gamma(c+n)} \frac{x^n}{n!} \]](form_140.png)
![\[ B(x, a, b ) = \frac{ \int_{0}^{x} u^{a-1} (1-u)^{b-1} du } { B(a,b) } \]](form_111.png)
![\[ P(a, x) = \frac{ 1} {\Gamma(a) } \int_{0}^{x} t^{a-1} e^{-t} dt \]](form_108.png)
![\[ Q(a, x) = \frac{ 1} {\Gamma(a) } \int_{x}^{\infty} t^{a-1} e^{-t} dt \]](form_109.png)
![\[ P_{l}(x) = \frac{ e^x}{n!} \frac{d^n}{dx^n} (x^n - e^{-x}) \]](form_141.png)
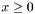 in the Rodrigues representation. They corresponds to the associated Laguerre polynomial of order m=0. See Abramowitz and Stegun, (22.5.16) For detailed description see
in the Rodrigues representation. They corresponds to the associated Laguerre polynomial of order m=0. See Abramowitz and Stegun, (22.5.16) For detailed description see ![\[ P_{l}(x) = \frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2 - 1)^l \]](form_143.png)
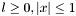 in the Rodrigues representation. For detailed description see
in the Rodrigues representation. For detailed description see ![\[ \zeta (x) = \left\{ \begin{array}{cl} \sum_{k=1}^{\infty}k^{-x} & \mbox{for $x > 1$} \\ 2^x \pi^{x-1} \sin{(\frac{1}{2}\pi x)} \Gamma(1-x) \zeta (1-x) & \mbox{for $x < 1$} \end{array} \right. \]](form_145.png)
![\[ Si(x) = - \int_{0}^{x} \frac{\sin t}{t} dt \]](form_112.png)
![\[ j_{n}(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x) \]](form_146.png)
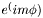 ).
).![\[ Y_l^m(theta,0) = \sqrt{(2l+1)/(4\pi)} \sqrt{(l-m)!/(l+m)!} P_l^m(cos \theta) \]](form_148.png)
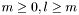 , where the Condon-Shortley phase
, where the Condon-Shortley phase ![\[ n_n(x) = y_n(x) = \sqrt{\frac{\pi}{2x}} N_{n+1/2}(x) \]](form_150.png)
![\[ \Gamma(x) = \int_{0}^{\infty} t^{x-1} e^{-t} dt \]](form_107.png)
 1.5.1
1.5.1