|
Functions |
| template<class T, unsigned int D> |
VecExpr< BinaryOp< AddOp<
T >, SVector< T, D >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator+ (const SVector< T, D > &lhs, const SVector< T, D > &rhs) |
| template<class A, class T, unsigned int D> |
VecExpr< BinaryOpCopyR< AddOp<
T >, SVector< T, D >, Constant<
A >, T >, T, D > | ROOT::Math::operator+ (const SVector< T, D > &lhs, const A &rhs) |
| template<class A, class T, unsigned int D> |
VecExpr< BinaryOpCopyL< AddOp<
T >, Constant< A >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator+ (const A &lhs, const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
VecExpr< BinaryOp< MinOp<
T >, SVector< T, D >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator- (const SVector< T, D > &lhs, const SVector< T, D > &rhs) |
| template<class A, class T, unsigned int D> |
VecExpr< BinaryOpCopyR< MinOp<
T >, SVector< T, D >, Constant<
A >, T >, T, D > | ROOT::Math::operator- (const SVector< T, D > &lhs, const A &rhs) |
| template<class A, class T, unsigned int D> |
VecExpr< BinaryOpCopyL< MinOp<
T >, Constant< A >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator- (const A &lhs, const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
VecExpr< BinaryOp< MulOp<
T >, SVector< T, D >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator * (const SVector< T, D > &lhs, const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
VecExpr< BinaryOp< DivOp<
T >, SVector< T, D >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator/ (const SVector< T, D > &lhs, const SVector< T, D > &rhs) |
| template<class A, class T, unsigned int D> |
VecExpr< BinaryOpCopyR< DivOp<
T >, SVector< T, D >, Constant<
A >, T >, T, D > | ROOT::Math::operator/ (const SVector< T, D > &lhs, const A &rhs) |
| template<class A, class T, unsigned int D> |
VecExpr< BinaryOpCopyL< DivOp<
T >, Constant< A >, SVector<
T, D >, T >, T, D > | ROOT::Math::operator/ (const A &lhs, const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
| T | ROOT::Math::Dot (const SVector< T, D > &lhs, const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
| T | ROOT::Math::Mag2 (const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
| T | ROOT::Math::Mag (const SVector< T, D > &rhs) |
| template<class T> |
| T | ROOT::Math::Lmag2 (const SVector< T, 4 > &rhs) |
| template<class T> |
| T | ROOT::Math::Lmag (const SVector< T, 4 > &rhs) |
| template<class T> |
| SVector< T, 3 > | ROOT::Math::Cross (const SVector< T, 3 > &lhs, const SVector< T, 3 > &rhs) |
| template<class T, unsigned int D> |
| SVector< T, D > | ROOT::Math::Unit (const SVector< T, D > &rhs) |
| template<class T, unsigned int D1, unsigned int D2> |
Expr< TensorMulOp< SVector<
T, D1 >, SVector< T, D2 > >,
T, D1, D2 > | ROOT::Math::TensorProd (const SVector< T, D1 > &lhs, const SVector< T, D2 > &rhs) |
| template<class T, unsigned int D> |
VecExpr< UnaryOp< Minus< T >,
SVector< T, D >, T >, T,
D > | ROOT::Math::operator- (const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
VecExpr< UnaryOp< Fabs< T >,
SVector< T, D >, T >, T,
D > | ROOT::Math::fabs (const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
VecExpr< UnaryOp< Sqr< T >,
SVector< T, D >, T >, T,
D > | ROOT::Math::sqr (const SVector< T, D > &rhs) |
| template<class T, unsigned int D> |
VecExpr< UnaryOp< Sqrt< T >,
SVector< T, D >, T >, T,
D > | ROOT::Math::sqrt (const SVector< T, D > &rhs) |
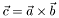 .
.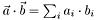 .
.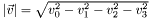 .
.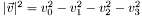 .
.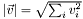 .
.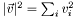 .
.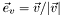 .
. 1.5.1
1.5.1