Probability Density Functions (PDF) from MathCore
[Statistical functions]


Probability Density Functions from MathCore

Additional PDF's are provided in the MathMore library (see PDF functions from MathMore)

double ROOT::Math::beta_pdf (double x, double a, double b)
double ROOT::Math::binomial_pdf (unsigned int k, double p, unsigned int n)
double ROOT::Math::negative_binomial_pdf (unsigned int k, double p, double n)
double ROOT::Math::breitwigner_pdf (double x, double gamma, double x0=0)
double ROOT::Math::cauchy_pdf (double x, double b=1, double x0=0)
double ROOT::Math::chisquared_pdf (double x, double r, double x0=0)
double ROOT::Math::exponential_pdf (double x, double lambda, double x0=0)
double ROOT::Math::fdistribution_pdf (double x, double n, double m, double x0=0)
double ROOT::Math::gamma_pdf (double x, double alpha, double theta, double x0=0)
double ROOT::Math::gaussian_pdf (double x, double sigma=1, double x0=0)
double ROOT::Math::landau_pdf (double x, double xi=1, double x0=0)
double ROOT::Math::lognormal_pdf (double x, double m, double s, double x0=0)
double ROOT::Math::normal_pdf (double x, double sigma=1, double x0=0)
double ROOT::Math::poisson_pdf (unsigned int n, double mu)
double ROOT::Math::tdistribution_pdf (double x, double r, double x0=0)
double ROOT::Math::uniform_pdf (double x, double a, double b, double x0=0)

Functions

double ROOT::Math::noncentral_chisquared_pdf (double x, double r, double lambda)
double ROOT::Math::vavilov_accurate_pdf (double x, double kappa, double beta2)
double ROOT::Math::vavilov_fast_pdf (double x, double kappa, double beta2)

Detailed Description

Probability density functions of various statistical distributions (continuous and discrete). The probability density function returns the probability that the variate has the value x. In statistics the PDF is also called the frequency function.

Function Documentation

double ROOT::Math::beta_pdf ( double  x,
double  a,
double  b 
)

Probability density function of the beta distribution.

\[ p(x) = \frac{\Gamma (a + b) } {\Gamma(a)\Gamma(b) } x ^{a-1} (1 - x)^{b-1} \]

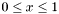for $0 \leq x \leq 1 $. For detailed description see Mathworld.

Definition at line 22 of file PdfFuncMathCore.cxx.

References exp(), RootCsg::infinity, ROOT::Math::lgamma(), log(), and ROOT::Math::log1p().

Referenced by G__G__MathCore_170_0_11(), G__setup_memfuncROOTcLcLMath(), mbeta_pdf(), rf105_funcbinding(), RooMathCoreReg::RooMathCoreReg(), testBetaFunction(), and TestBasic105::testCode().

double ROOT::Math::binomial_pdf ( unsigned int  k,
double  p,
unsigned int  n 
)

Probability density function of the binomial distribution.

\[ p(k) = \frac{n!}{k! (n-k)!} p^k (1-p)^{n-k} \]

for 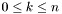$ 0 \leq k \leq n $. For detailed description see Mathworld.

Definition at line 40 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::lgamma(), log(), and ROOT::Math::log1p().

Referenced by binomial_pmf(), G__G__MathCore_170_0_12(), G__setup_memfuncROOTcLcLMath(), RooMathCoreReg::RooMathCoreReg(), and testBinomialCdf().

double ROOT::Math::breitwigner_pdf ( double  x,
double  gamma,
double  x0 = 0 
)

Probability density function of Breit-Wigner distribution, which is similar, just a different definition of the parameters, to the Cauchy distribution (see cauchy_pdf )

\[ p(x) = \frac{1}{\pi} \frac{\frac{1}{2} \Gamma}{x^2 + (\frac{1}{2} \Gamma)^2} \]

Definition at line 63 of file PdfFuncMathCore.cxx.

References M_PI.

Referenced by distr(), G__G__MathCore_170_0_14(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::cauchy_pdf ( double  x,
double  b = 1,
double  x0 = 0 
)

Probability density function of the Cauchy distribution which is also called Lorentzian distribution.

\[ p(x) = \frac{1}{\pi} \frac{ b }{ (x-m)^2 + b^2} \]

For detailed description see Mathworld. It is also related to the breitwigner_pdf which will call the same implementation.

Definition at line 73 of file PdfFuncMathCore.cxx.

References M_PI.

Referenced by G__G__MathCore_170_0_15(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::chisquared_pdf ( double  x,
double  r,
double  x0 = 0 
)

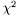Probability density function of the $\chi^2$ distribution with 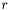$r$ degrees of freedom.

\[ p_r(x) = \frac{1}{\Gamma(r/2) 2^{r/2}} x^{r/2-1} e^{-x/2} \]

for 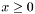$x \geq 0$. For detailed description see Mathworld.

Definition at line 81 of file PdfFuncMathCore.cxx.

References a, exp(), ROOT::Math::lgamma(), and log().

Referenced by RooNonCentralChiSquare::evaluate(), G__G__MathCore_170_0_16(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::noncentral_chisquared_pdf(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::exponential_pdf ( double  x,
double  lambda,
double  x0 = 0 
)

Probability density function of the exponential distribution.

\[ p(x) = \lambda e^{-\lambda x} \]

for x>0. For detailed description see Mathworld.

Definition at line 96 of file PdfFuncMathCore.cxx.

References exp().

Referenced by G__G__MathCore_170_0_17(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::fdistribution_pdf ( double  x,
double  n,
double  m,
double  x0 = 0 
)

Probability density function of the F-distribution.

\[ p_{n,m}(x) = \frac{\Gamma(\frac{n+m}{2})}{\Gamma(\frac{n}{2}) \Gamma(\frac{m}{2})} n^{n/2} m^{m/2} x^{n/2 -1} (m+nx)^{-(n+m)/2} \]

for x>=0. For detailed description see Mathworld.

Definition at line 108 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::lgamma(), and log().

Referenced by TMath::FDist(), G__G__MathCore_170_0_18(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::gamma_pdf ( double  x,
double  alpha,
double  theta,
double  x0 = 0 
)

Probability density function of the gamma distribution.

\[ p(x) = {1 \over \Gamma(\alpha) \theta^{\alpha}} x^{\alpha-1} e^{-x/\theta} \]

for x>0. For detailed description see Mathworld.

Definition at line 123 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::lgamma(), and log().

Referenced by G__G__MathCore_170_0_19(), G__setup_memfuncROOTcLcLMath(), TMath::GammaDist(), RooMathCoreReg::RooMathCoreReg(), and testGammaFunction().

double ROOT::Math::gaussian_pdf ( double  x,
double  sigma = 1,
double  x0 = 0 
)

Probability density function of the normal (Gaussian) distribution.

\[ p(x) = {1 \over \sqrt{2 \pi \sigma^2}} e^{-x^2 / 2\sigma^2} \]

For detailed description see Mathworld. It can also be evaluated using normal_pdf which will call the same implementation.

Definition at line 145 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::fabs(), M_PI, and sqrt().

Referenced by G__G__MathCore_170_0_20(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::landau_pdf ( double  x,
double  xi = 1,
double  x0 = 0 
)

Probability density function of the Landau distribution:

\[ p(x) = \frac{1}{\xi} \phi (\lambda) \]

with

\[ \phi(\lambda) = \frac{1}{2 \pi i}\int_{c-i\infty}^{c+i\infty} e^{\lambda s + s \log{s}} ds\]

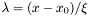where $\lambda = (x-x_0)/\xi$. For a detailed description see K.S. Kölbig and B. Schorr, A program package for the Landau distribution, Computer Phys. Comm. 31 (1984) 97-111 [Erratum-ibid. 178 (2008) 972]. The same algorithms as in CERNLIB (DENLAN) is used

Parameters:
x The argument $x$
xi The width parameter $\xi$
x0 The location parameter $x_0$

Definition at line 153 of file PdfFuncMathCore.cxx.

References exp(), log(), p1(), p2(), p3(), p4(), sqrt(), and u.

Referenced by G__G__MathCore_170_0_21(), G__setup_memfuncROOTcLcLMath(), TMath::Landau(), ROOT::Math::VavilovFast::Pdf(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::lognormal_pdf ( double  x,
double  m,
double  s,
double  x0 = 0 
)

Probability density function of the lognormal distribution.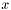

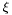
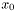
\[ p(x) = {1 \over x \sqrt{2 \pi s^2} } e^{-(\ln{x} - m)^2/2 s^2} \]

for x>0. For detailed description see Mathworld.

Parameters:
s scale parameter (not the sigma of the distribution which is not even defined)
x0 location parameter, corresponds approximatly to the most probable value. For x0 = 0, sigma = 1, the x_mpv = -0.22278

Definition at line 223 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::fabs(), log(), M_PI, and sqrt().

Referenced by RooLognormal::evaluate(), G__G__MathCore_170_0_22(), G__setup_memfuncROOTcLcLMath(), TMath::LogNormal(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::negative_binomial_pdf ( unsigned int  k,
double  p,
double  n 
)

Probability density function of the negative binomial distribution.

\[ p(k) = \frac{(k+n-1)!}{k! (n-1)!} p^{n} (1-p)^{k} \]

For detailed description see Mathworld (where $k x$ and $n r$). The distribution in Wikipedia is defined with a $p$ corresponding to $1-p$ in this case.

Definition at line 51 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::lgamma(), log(), and ROOT::Math::log1p().

Referenced by G__G__MathCore_170_0_13(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::noncentral_chisquared_pdf ( double  x,
double  r,
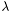
double  lambda 
)

Probability density function of the non central $\chi^2$ distribution with $r$ degrees of freedom and the noon-central parameter $\lambda$

\[ p_r(x) = \frac{1}{\Gamma(r/2) 2^{r/2}} x^{r/2-1} e^{-x/2} \]

for $x \geq 0$. For detailed description see Mathworld.

Definition at line 22 of file PdfFuncMathMore.cxx.

References ROOT::Math::chisquared_pdf(), ROOT::Math::cyl_bessel_i(), exp(), pow(), sqrt(), and ROOT::Math::tgamma().

Referenced by RooNonCentralChiSquare::evaluate(), G__G__MathMore_99_0_1(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::normal_pdf ( double  x,
double  sigma = 1,
double  x0 = 0 
)

Probability density function of the normal (Gaussian) distribution.

\[ p(x) = {1 \over \sqrt{2 \pi \sigma^2}} e^{-x^2 / 2\sigma^2} \]

For detailed description see Mathworld. It can also be evaluated using gaussian_pdf which will call the same implementation.

Definition at line 236 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::fabs(), M_PI, and sqrt().

Referenced by G__G__MathCore_170_0_23(), G__setup_memfuncROOTcLcLMath(), gausNd(), norm(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::poisson_pdf ( unsigned int  n,
double  mu 
)

Probability density function of the Poisson distribution.

\[ p(n) = \frac{\mu^n}{n!} e^{- \mu} \]

For detailed description see Mathworld.

Definition at line 245 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::lgamma(), and log().

Referenced by G__G__MathCore_170_0_24(), G__setup_memfuncROOTcLcLMath(), poisson(), poisson_pmf(), RooMathCoreReg::RooMathCoreReg(), and testPoissonCdf().

double ROOT::Math::tdistribution_pdf ( double  x,
double  r,
double  x0 = 0 
)

Probability density function of Student's t-distribution.

\[ p_{r}(x) = \frac{\Gamma(\frac{r+1}{2})}{\sqrt{r \pi}\Gamma(\frac{r}{2})} \left( 1+\frac{x^2}{r}\right)^{-(r+1)/2} \]

for 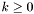$k \geq 0$. For detailed description see Mathworld.

Definition at line 260 of file PdfFuncMathCore.cxx.

References exp(), ROOT::Math::lgamma(), M_PI, pow(), and sqrt().

Referenced by G__G__MathCore_170_0_25(), G__setup_memfuncROOTcLcLMath(), RooMathCoreReg::RooMathCoreReg(), and tStudent().

double ROOT::Math::uniform_pdf ( double  x,
double  a,
double  b,
double  x0 = 0 
)

Probability density function of the uniform (flat) distribution.

\[ p(x) = {1 \over (b-a)} \]

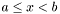if $a \leq x<b$ and 0 otherwise. For detailed description see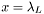 Mathworld.

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! when a=b

Definition at line 269 of file PdfFuncMathCore.cxx.

Referenced by G__G__MathCore_170_0_26(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::vavilov_accurate_pdf ( double  x,
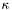double  kappa,
double  beta2 
)

The Vavilov probability density function

Parameters:
x The Landau parameter $x = \lambda_L$
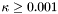
kappa The parameter $\kappa$, which must be in the range $\kappa \ge 0.001 $
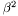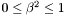
beta2 The parameter $\beta^2$, which must be in the range $0 \le \beta^2 \le 1 $

Definition at line 462 of file VavilovAccurate.cxx.

References ROOT::Math::VavilovAccurate::GetInstance(), and vavilov().

Referenced by G__G__MathMore_99_0_37(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::vavilov_fast_pdf ( double  x,
double  kappa,
double  beta2 
)

The Vavilov probability density function

Parameters:
x The Landau parameter $x = \lambda_L$
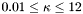
kappa The parameter $\kappa$, which must be in the range $0.01 \le \kappa \le 12 $
beta2 The parameter $\beta^2$, which must be in the range $0 \le \beta^2 \le 1 $

Definition at line 578 of file VavilovFast.cxx.

References ROOT::Math::VavilovFast::GetInstance(), and vavilov().

Referenced by G__G__MathMore_99_0_42(), and G__setup_memfuncROOTcLcLMath().

Generated on Tue Jul 5 16:09:42 2011 for ROOT_528-00b_version by  doxygen 1.5.1