![\[ D(x) = \int_{-\infty}^{x} p(x') dx' \]](form_73.png)
 where
where
![\[ D(x) = \int_{-\infty}^{x} p(x') dx' \]](form_73.png)
while those with the _quantile_c extension calculate the inverse of the _cdf_c functions, the upper tail integral of the probability density function 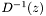 where
where
![\[ D(x) = \int_{x}^{+\infty} p(x') dx' \]](form_74.png)
These functions are defined in the header file Math/ProbFunc.h or in the global one including all statistical dunctions Math/DistFunc.h
NOTE: In the old releases (< 5.14) the _quantile functions were called _quant_inv and the _quantile_c functions were called _prob_inv. These names are currently kept for backward compatibility, but their usage is deprecated.
Inverse ( ) of the cumulative distribution function of the upper tail of the beta distribution (beta_cdf_c). It is implemented using the function incbi from Cephes.
) of the cumulative distribution function of the upper tail of the beta distribution (beta_cdf_c). It is implemented using the function incbi from Cephes.
Definition at line 26 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::incbi().
Referenced by TEfficiency::BetaCentralInterval(), TEfficiency::BetaShortestInterval(), TEfficiency::ClopperPearson(), G__G__MathCore_170_0_61(), G__setup_memfuncROOTcLcLMath(), mbeta_quantile(), Beta_interval_length::operator()(), RooMathCoreReg::RooMathCoreReg(), and testBetaFunction().
Inverse ( ) of the cumulative distribution function of the lower tail of the beta distribution (beta_cdf). It is implemented using the function incbi from Cephes.
) of the cumulative distribution function of the lower tail of the beta distribution (beta_cdf). It is implemented using the function incbi from Cephes.
Definition at line 16 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::incbi().
Referenced by TEfficiency::BetaShortestInterval(), G__G__MathCore_170_0_62(), G__setup_memfuncROOTcLcLMath(), Beta_interval_length::LowerMax(), mbeta_quantile_c(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the Breit_Wigner distribution (breitwigner_cdf) which is similar to the Cauchy distribution. For detailed description see Mathworld. It is evaluated using the same implementation of cauchy_quantile.
) of the cumulative distribution function of the lower tail of the Breit_Wigner distribution (breitwigner_cdf) which is similar to the Cauchy distribution. For detailed description see Mathworld. It is evaluated using the same implementation of cauchy_quantile.
Definition at line 178 of file QuantFuncMathCore.h.
References ROOT::Math::cauchy_quantile().
Referenced by G__G__MathCore_170_0_66(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the upper tail of the Breit-Wigner distribution (breitwigner_cdf_c) which is similar to the Cauchy distribution. For detailed description see Mathworld. It is evaluated using the same implementation of cauchy_quantile_c.
) of the cumulative distribution function of the upper tail of the Breit-Wigner distribution (breitwigner_cdf_c) which is similar to the Cauchy distribution. For detailed description see Mathworld. It is evaluated using the same implementation of cauchy_quantile_c.
Definition at line 156 of file QuantFuncMathCore.h.
References ROOT::Math::cauchy_quantile_c().
Referenced by G__G__MathCore_170_0_65(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the Cauchy distribution (cauchy_cdf) which is also called Breit-Wigner or Lorentzian distribution. For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the lower tail of the Cauchy distribution (cauchy_cdf) which is also called Breit-Wigner or Lorentzian distribution. For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 46 of file QuantFuncMathCore.cxx.
References RootCsg::infinity, M_PI, and tan().
Referenced by ROOT::Math::breitwigner_quantile(), G__G__MathCore_170_0_64(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the upper tail of the Cauchy distribution (cauchy_cdf_c) which is also called Lorentzian distribution. For detailed description see Mathworld.
) of the cumulative distribution function of the upper tail of the Cauchy distribution (cauchy_cdf_c) which is also called Lorentzian distribution. For detailed description see Mathworld.
Definition at line 33 of file QuantFuncMathCore.cxx.
References RootCsg::infinity, M_PI, and tan().
Referenced by ROOT::Math::breitwigner_quantile_c(), G__G__MathCore_170_0_63(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Re-implementation in MathMore of the Inverse ( ) of the cumulative distribution function of the lower tail of the
) of the cumulative distribution function of the lower tail of the 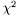 distribution with
distribution with 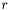 degrees of freedom (chisquared_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
degrees of freedom (chisquared_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 31 of file QuantFuncMathMore.cxx.
References ROOT::Math::Cephes::igami().
Referenced by G__G__MathCore_170_0_68(), G__G__MathMore_100_0_1(), G__setup_memfuncROOTcLcLMath(), G__setup_memfuncROOTcLcLMathMore(), and ROOT::Fit::FitResult::GetConfidenceIntervals().
Re-implementation in MathMore of the Inverse ( ) of the cumulative distribution function of the lower tail of the
) of the cumulative distribution function of the lower tail of the 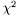 distribution with
distribution with 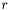 degrees of freedom (chisquared_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
degrees of freedom (chisquared_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 67 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::igami().
Referenced by G__G__MathCore_170_0_68(), G__G__MathMore_100_0_1(), G__setup_memfuncROOTcLcLMath(), G__setup_memfuncROOTcLcLMathMore(), and ROOT::Fit::FitResult::GetConfidenceIntervals().
Inverse ( ) of the cumulative distribution function of the upper tail of the
) of the cumulative distribution function of the upper tail of the 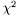 distribution with
distribution with 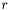 degrees of freedom (chisquared_cdf_c). For detailed description see Mathworld. It is implemented using the inverse of the incomplete complement gamma function, using the function igami from Cephes.
degrees of freedom (chisquared_cdf_c). For detailed description see Mathworld. It is implemented using the inverse of the incomplete complement gamma function, using the function igami from Cephes.
Definition at line 60 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::igami().
Referenced by G__G__MathCore_170_0_67(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the exponential distribution (exponential_cdf). For detailed description see Mathworld.
) of the cumulative distribution function of the lower tail of the exponential distribution (exponential_cdf). For detailed description see Mathworld.
Definition at line 82 of file QuantFuncMathCore.cxx.
References ROOT::Math::log1p().
Referenced by G__G__MathCore_170_0_70(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the upper tail of the exponential distribution (exponential_cdf_c). For detailed description see Mathworld.
) of the cumulative distribution function of the upper tail of the exponential distribution (exponential_cdf_c). For detailed description see Mathworld.
Definition at line 74 of file QuantFuncMathCore.cxx.
References log().
Referenced by G__G__MathCore_170_0_69(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the f distribution (fdistribution_cdf). For detailed description see Mathworld. It is implemented using the inverse of the incomplete beta function, function incbi from Cephes.
) of the cumulative distribution function of the lower tail of the f distribution (fdistribution_cdf). For detailed description see Mathworld. It is implemented using the inverse of the incomplete beta function, function incbi from Cephes.
Definition at line 103 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::incbi(), and y.
Referenced by G__G__MathCore_170_0_71(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the upper tail of the f distribution (fdistribution_cdf_c). For detailed description see Mathworld. It is implemented using the inverse of the incomplete beta function, function incbi from Cephes.
) of the cumulative distribution function of the upper tail of the f distribution (fdistribution_cdf_c). For detailed description see Mathworld. It is implemented using the inverse of the incomplete beta function, function incbi from Cephes.
Definition at line 89 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::incbi(), and y.
Referenced by G__G__MathCore_170_0_72(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Re-implementation in MathMore of the Inverse ( ) of the cumulative distribution function of the lower tail of the gamma distribution (gamma_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the lower tail of the gamma distribution (gamma_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 38 of file QuantFuncMathMore.cxx.
References ROOT::Math::Cephes::igami().
Referenced by G__G__MathCore_170_0_74(), G__G__MathMore_100_0_2(), G__setup_memfuncROOTcLcLMath(), G__setup_memfuncROOTcLcLMathMore(), and testGammaFunction().
Re-implementation in MathMore of the Inverse ( ) of the cumulative distribution function of the lower tail of the gamma distribution (gamma_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the lower tail of the gamma distribution (gamma_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 118 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::igami().
Referenced by G__G__MathCore_170_0_74(), G__G__MathMore_100_0_2(), G__setup_memfuncROOTcLcLMath(), G__setup_memfuncROOTcLcLMathMore(), and testGammaFunction().
Inverse ( ) of the cumulative distribution function of the upper tail of the gamma distribution (gamma_cdf_c). For detailed description see Mathworld. The implementation used is that of GSL. It is implemented using the function igami taken from Cephes.
) of the cumulative distribution function of the upper tail of the gamma distribution (gamma_cdf_c). For detailed description see Mathworld. The implementation used is that of GSL. It is implemented using the function igami taken from Cephes.
Definition at line 112 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::igami().
Referenced by G__G__MathCore_170_0_73(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
alternative name for same function
Inverse ( ) of the cumulative distribution function of the lower tail of the normal (Gaussian) distribution (gaussian_cdf). For detailed description see Mathworld. It can also be evaluated using normal_quantile which will call the same implementation. It is implemented using the function ROOT::Math::Cephes::ndtri taken from Cephes.
) of the cumulative distribution function of the lower tail of the normal (Gaussian) distribution (gaussian_cdf). For detailed description see Mathworld. It can also be evaluated using normal_quantile which will call the same implementation. It is implemented using the function ROOT::Math::Cephes::ndtri taken from Cephes.
Definition at line 442 of file QuantFuncMathCore.h.
References ROOT::Math::normal_quantile().
Referenced by G__G__MathCore_170_0_76(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
alternative name for same function
Inverse ( ) of the cumulative distribution function of the upper tail of the normal (Gaussian) distribution (gaussian_cdf_c). For detailed description see Mathworld. It can also be evaluated using normal_quantile_c which will call the same implementation.
) of the cumulative distribution function of the upper tail of the normal (Gaussian) distribution (gaussian_cdf_c). For detailed description see Mathworld. It can also be evaluated using normal_quantile_c which will call the same implementation.
Definition at line 417 of file QuantFuncMathCore.h.
References ROOT::Math::normal_quantile_c().
Referenced by G__G__MathCore_170_0_75(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the Landau distribution (landau_cdf).
) of the cumulative distribution function of the lower tail of the Landau distribution (landau_cdf).
For detailed description see K.S. Kölbig and B. Schorr, A program package for the Landau distribution, Computer Phys. Comm. 31 (1984) 97-111 [Erratum-ibid. 178 (2008) 972]. The same algorithms as in CERNLIB (RANLAN) is used.
| z | The argument 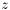 | |
| xi | The width parameter 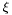 |
Definition at line 189 of file QuantFuncMathCore.cxx.
References i, RootCsg::infinity, int, log(), and u.
Referenced by G__G__MathCore_170_0_83(), G__setup_memfuncROOTcLcLMath(), TRandom::Landau(), ROOT::Math::landau_quantile_c(), ROOT::Math::VavilovAccurate::Quantile(), and ROOT::Math::VavilovAccurate::Quantile_c().
Inverse ( ) of the cumulative distribution function of the upper tail of the landau distribution (landau_cdf_c). Implemented using landau_quantile
) of the cumulative distribution function of the upper tail of the landau distribution (landau_cdf_c). Implemented using landau_quantile
| z | The argument 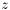 | |
| xi | The width parameter 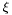 |
Definition at line 396 of file QuantFuncMathCore.cxx.
References ROOT::Math::landau_quantile().
Referenced by G__G__MathCore_170_0_84(), and G__setup_memfuncROOTcLcLMath().
Inverse ( ) of the cumulative distribution function of the lower tail of the lognormal distribution (lognormal_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the lower tail of the lognormal distribution (lognormal_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 151 of file QuantFuncMathCore.cxx.
References exp(), ROOT::Math::Cephes::ndtri(), and y.
Referenced by G__G__MathCore_170_0_78(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the upper tail of the lognormal distribution (lognormal_cdf_c). For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the upper tail of the lognormal distribution (lognormal_cdf_c). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 143 of file QuantFuncMathCore.cxx.
References exp(), ROOT::Math::Cephes::ndtri(), and y.
Referenced by G__G__MathCore_170_0_77(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the normal (Gaussian) distribution (normal_cdf). For detailed description see Mathworld. It can also be evaluated using gaussian_quantile which will call the same implementation. It is implemented using the function ROOT::Math::Cephes::ndtri taken from Cephes.
) of the cumulative distribution function of the lower tail of the normal (Gaussian) distribution (normal_cdf). For detailed description see Mathworld. It can also be evaluated using gaussian_quantile which will call the same implementation. It is implemented using the function ROOT::Math::Cephes::ndtri taken from Cephes.
Definition at line 134 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::ndtri().
Referenced by TEfficiency::AgrestiCoull(), G__G__MathCore_170_0_80(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::gaussian_quantile(), IntervalExamples(), TKDE::LowerConfidenceInterval(), TEfficiency::Normal(), RooMathCoreReg::RooMathCoreReg(), TKDE::UpperConfidenceInterval(), and TEfficiency::Wilson().
Inverse ( ) of the cumulative distribution function of the upper tail of the normal (Gaussian) distribution (normal_cdf_c). For detailed description see Mathworld. It can also be evaluated using gaussian_quantile_c which will call the same implementation. It is implemented using the function ROOT::Math::Cephes::ndtri taken from Cephes.
) of the cumulative distribution function of the upper tail of the normal (Gaussian) distribution (normal_cdf_c). For detailed description see Mathworld. It can also be evaluated using gaussian_quantile_c which will call the same implementation. It is implemented using the function ROOT::Math::Cephes::ndtri taken from Cephes.
Definition at line 126 of file QuantFuncMathCore.cxx.
References ROOT::Math::Cephes::ndtri().
Referenced by TGraphAsymmErrors::Divide(), G__G__MathCore_170_0_79(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::gaussian_quantile_c(), IntervalExamples(), RooStats::PValueToSignificance(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of Student's t-distribution (tdistribution_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the lower tail of Student's t-distribution (tdistribution_cdf). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 20 of file QuantFuncMathMore.cxx.
Referenced by G__G__MathMore_99_0_3(), G__setup_memfuncROOTcLcLMath(), RooMathMoreReg::RooMathMoreReg(), and tStudent().
Inverse ( ) of the cumulative distribution function of the upper tail of Student's t-distribution (tdistribution_cdf_c). For detailed description see Mathworld. The implementation used is that of GSL.
) of the cumulative distribution function of the upper tail of Student's t-distribution (tdistribution_cdf_c). For detailed description see Mathworld. The implementation used is that of GSL.
Definition at line 12 of file QuantFuncMathMore.cxx.
Referenced by G__G__MathMore_99_0_2(), G__setup_memfuncROOTcLcLMath(), and RooMathMoreReg::RooMathMoreReg().
Inverse ( ) of the cumulative distribution function of the lower tail of the uniform (flat) distribution (uniform_cdf). For detailed description see Mathworld.
) of the cumulative distribution function of the lower tail of the uniform (flat) distribution (uniform_cdf). For detailed description see Mathworld.
Definition at line 183 of file QuantFuncMathCore.cxx.
Referenced by G__G__MathCore_170_0_82(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
Inverse ( ) of the cumulative distribution function of the upper tail of the uniform (flat) distribution (uniform_cdf_c). For detailed description see Mathworld.
) of the cumulative distribution function of the upper tail of the uniform (flat) distribution (uniform_cdf_c). For detailed description see Mathworld.
Definition at line 175 of file QuantFuncMathCore.cxx.
Referenced by G__G__MathCore_170_0_81(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().
The inverse of the Vavilov cummulative probability density function
| z | The argument 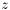 , which must be in the range , which must be in the range 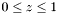 | |
| kappa | The parameter 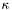 , which must be in the range , which must be in the range 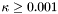 | |
| beta2 | The parameter 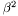 , which must be in the range , which must be in the range 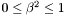 |
Definition at line 477 of file VavilovAccurate.cxx.
References ROOT::Math::VavilovAccurate::GetInstance(), and vavilov().
Referenced by G__G__MathMore_99_0_40(), and G__setup_memfuncROOTcLcLMath().
The inverse of the complementary Vavilov cummulative probability density function
| z | The argument 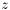 , which must be in the range , which must be in the range 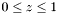 | |
| kappa | The parameter 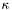 , which must be in the range , which must be in the range 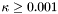 | |
| beta2 | The parameter 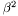 , which must be in the range , which must be in the range 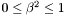 |
Definition at line 482 of file VavilovAccurate.cxx.
References ROOT::Math::VavilovAccurate::GetInstance(), and vavilov().
Referenced by G__G__MathMore_99_0_41(), and G__setup_memfuncROOTcLcLMath().
The inverse of the Vavilov cummulative probability density function
| z | The argument 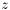 , which must be in the range , which must be in the range 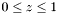 | |
| kappa | The parameter 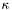 , which must be in the range , which must be in the range 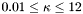 | |
| beta2 | The parameter 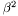 , which must be in the range , which must be in the range 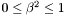 |
Definition at line 593 of file VavilovFast.cxx.
References ROOT::Math::VavilovFast::GetInstance(), and vavilov().
Referenced by G__G__MathMore_99_0_45(), and G__setup_memfuncROOTcLcLMath().
The inverse of the complementary Vavilov cummulative probability density function
| z | The argument 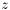 , which must be in the range , which must be in the range 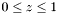 | |
| kappa | The parameter 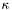 , which must be in the range , which must be in the range 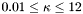 | |
| beta2 | The parameter 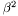 , which must be in the range , which must be in the range 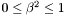 |
Definition at line 598 of file VavilovFast.cxx.
References ROOT::Math::VavilovFast::GetInstance(), and vavilov().
Referenced by G__G__MathMore_99_0_46(), and G__setup_memfuncROOTcLcLMath().
 1.5.1
1.5.1