Cumulative Distribution Functions (CDF)
[Statistical functions]


Functions

double ROOT::Math::beta_cdf_c (double x, double a, double b)
double ROOT::Math::beta_cdf (double x, double a, double b)
double ROOT::Math::breitwigner_cdf_c (double x, double gamma, double x0=0)
double ROOT::Math::breitwigner_cdf (double x, double gamma, double x0=0)
double ROOT::Math::cauchy_cdf_c (double x, double b, double x0=0)
double ROOT::Math::cauchy_cdf (double x, double b, double x0=0)
double ROOT::Math::chisquared_cdf_c (double x, double r, double x0=0)
double ROOT::Math::chisquared_cdf (double x, double r, double x0=0)
double ROOT::Math::exponential_cdf_c (double x, double lambda, double x0=0)
double ROOT::Math::exponential_cdf (double x, double lambda, double x0=0)
double ROOT::Math::fdistribution_cdf_c (double x, double n, double m, double x0=0)
double ROOT::Math::fdistribution_cdf (double x, double n, double m, double x0=0)
double ROOT::Math::gamma_cdf_c (double x, double alpha, double theta, double x0=0)
double ROOT::Math::gamma_cdf (double x, double alpha, double theta, double x0=0)
double ROOT::Math::landau_cdf (double x, double xi=1, double x0=0)
double ROOT::Math::landau_cdf_c (double x, double xi=1, double x0=0)
double ROOT::Math::lognormal_cdf_c (double x, double m, double s, double x0=0)
double ROOT::Math::lognormal_cdf (double x, double m, double s, double x0=0)
double ROOT::Math::normal_cdf_c (double x, double sigma=1, double x0=0)
double ROOT::Math::normal_cdf (double x, double sigma=1, double x0=0)
double ROOT::Math::tdistribution_cdf_c (double x, double r, double x0=0)
double ROOT::Math::tdistribution_cdf (double x, double r, double x0=0)
double ROOT::Math::uniform_cdf_c (double x, double a, double b, double x0=0)
double ROOT::Math::uniform_cdf (double x, double a, double b, double x0=0)
double ROOT::Math::poisson_cdf_c (unsigned int n, double mu)
 discrete distributions
double ROOT::Math::poisson_cdf (unsigned int n, double mu)
double ROOT::Math::binomial_cdf_c (unsigned int k, double p, unsigned int n)
double ROOT::Math::binomial_cdf (unsigned int k, double p, unsigned int n)
double ROOT::Math::negative_binomial_cdf_c (unsigned int k, double p, double n)
double ROOT::Math::negative_binomial_cdf (unsigned int k, double p, double n)
double ROOT::Math::vavilov_accurate_cdf (double x, double kappa, double beta2)
double ROOT::Math::vavilov_accurate_cdf_c (double x, double kappa, double beta2)
double ROOT::Math::vavilov_fast_cdf (double x, double kappa, double beta2)
double ROOT::Math::vavilov_fast_cdf_c (double x, double kappa, double beta2)

Detailed Description

Cumulative distribution functions of various distributions. The functions with the extension _cdf calculate the lower tail integral of the probability density function

\[ D(x) = \int_{-\infty}^{x} p(x') dx' \]

while those with the _cdf_c extension calculate the complement of cumulative distribution function, called in statistics the survival function. It corresponds to the upper tail integral of the probability density function

\[ D(x) = \int_{x}^{+\infty} p(x') dx' \]

NOTE: In the old releases (< 5.14) the _cdf functions were called _quant and the _cdf_c functions were called _prob. These names are currently kept for backward compatibility, but their usage is deprecated.

These functions are defined in the header file Math/ProbFunc.h or in the global one including all statistical dunctions Math/DistFunc.h

Function Documentation

double ROOT::Math::beta_cdf ( double  x,
double  a,
double  b 
)

Cumulative distribution function of the beta distribution Upper tail of the integral of the beta_pdf

Definition at line 23 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_beta().

Referenced by ROOT::Math::binomial_cdf_c(), G__G__MathCore_170_0_28(), G__setup_memfuncROOTcLcLMath(), mbeta_cdf(), ROOT::Math::negative_binomial_cdf(), Beta_interval_length::operator()(), RooMathCoreReg::RooMathCoreReg(), and testBetaFunction().

double ROOT::Math::beta_cdf_c ( double  x,
double  a,
double  b 
)

Complement of the cumulative distribution function of the beta distribution. Upper tail of the integral of the beta_pdf

Definition at line 17 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_beta().

Referenced by ROOT::Math::binomial_cdf(), G__G__MathCore_170_0_27(), G__setup_memfuncROOTcLcLMath(), mbeta_cdf_c(), ROOT::Math::negative_binomial_cdf_c(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::binomial_cdf ( unsigned int  k,
double  p,
unsigned int  n 
)

Cumulative distribution function of the Binomial distribution Lower tail of the integral of the binomial_pdf

Definition at line 272 of file ProbFuncMathCore.cxx.

References a, b, ROOT::Math::beta_cdf_c(), and double.

Referenced by G__G__MathCore_170_0_56(), G__setup_memfuncROOTcLcLMath(), RooMathCoreReg::RooMathCoreReg(), and testBinomialCdf().

double ROOT::Math::binomial_cdf_c ( unsigned int  k,
double  p,
unsigned int  n 
)

Complement of the cumulative distribution function of the Binomial distribution. Upper tail of the integral of the binomial_pdf

Definition at line 262 of file ProbFuncMathCore.cxx.

References a, b, ROOT::Math::beta_cdf(), and double.

Referenced by G__G__MathCore_170_0_55(), G__setup_memfuncROOTcLcLMath(), RooMathCoreReg::RooMathCoreReg(), and testBinomialCdf().

double ROOT::Math::breitwigner_cdf ( double  x,
double  gamma,
double  x0 = 0 
)

Cumulative distribution function (lower tail) of the Breit_Wigner distribution and it is similar (just a different parameter definition) to the Cauchy distribution (see cauchy_cdf )

\[ D(x) = \int_{-\infty}^{x} \frac{1}{\pi} \frac{b}{x'^2 + (\frac{1}{2} \Gamma)^2} dx' \]

Definition at line 39 of file ProbFuncMathCore.cxx.

References atan(), and M_PI.

Referenced by cdf(), G__G__MathCore_170_0_30(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::breitwigner_cdf_c ( double  x,
double  gamma,
double  x0 = 0 
)

Complement of the cumulative distribution function (upper tail) of the Breit_Wigner distribution and it is similar (just a different parameter definition) to the Cauchy distribution (see cauchy_cdf_c )

\[ D(x) = \int_{x}^{+\infty} \frac{1}{\pi} \frac{\frac{1}{2} \Gamma}{x'^2 + (\frac{1}{2} \Gamma)^2} dx' \]

Definition at line 31 of file ProbFuncMathCore.cxx.

References atan(), and M_PI.

Referenced by G__G__MathCore_170_0_29(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::cauchy_cdf ( double  x,
double  b,
double  x0 = 0 
)

Cumulative distribution function (lower tail) of the Cauchy distribution which is also Lorentzian distribution. It is similar (just a different parameter definition) to the Breit_Wigner distribution (see breitwigner_cdf )

\[ D(x) = \int_{-\infty}^{x} \frac{1}{\pi} \frac{ b }{ (x'-m)^2 + b^2} dx' \]

For detailed description see Mathworld.

Definition at line 55 of file ProbFuncMathCore.cxx.

References atan(), and M_PI.

Referenced by G__G__MathCore_170_0_32(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::cauchy_cdf_c ( double  x,
double  b,
double  x0 = 0 
)

Complement of the cumulative distribution function (upper tail) of the Cauchy distribution which is also Lorentzian distribution. It is similar (just a different parameter definition) to the Breit_Wigner distribution (see breitwigner_cdf_c )

\[ D(x) = \int_{x}^{+\infty} \frac{1}{\pi} \frac{ b }{ (x'-m)^2 + b^2} dx' \]

For detailed description see Mathworld.

Definition at line 47 of file ProbFuncMathCore.cxx.

References atan(), and M_PI.

Referenced by G__G__MathCore_170_0_31(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::chisquared_cdf ( double  x,
double  r,
double  x0 = 0 
)

Cumulative distribution function of the 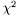$\chi^2$ distribution with 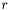$r$ degrees of freedom (lower tail).

\[ D_{r}(x) = \int_{-\infty}^{x} \frac{1}{\Gamma(r/2) 2^{r/2}} x'^{r/2-1} e^{-x'/2} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete gamma function, ROOT::Math::inc_gamma_c, from Cephes

Definition at line 69 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_gamma().

Referenced by RooNonCentralChiSquare::analyticalIntegral(), G__G__MathCore_170_0_34(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::chisquared_cdf_c ( double  x,
double  r,
double  x0 = 0 
)

Complement of the cumulative distribution function of the 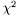$\chi^2$ distribution with 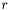$r$ degrees of freedom (upper tail).

\[ D_{r}(x) = \int_{x}^{+\infty} \frac{1}{\Gamma(r/2) 2^{r/2}} x'^{r/2-1} e^{-x'/2} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete gamma function, ROOT::Math::inc_gamma_c, from Cephes

Definition at line 63 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_gamma_c().

Referenced by DoUnBinFit(), G__G__MathCore_170_0_33(), G__setup_memfuncROOTcLcLMath(), TMath::Prob(), ROOT::Fit::FitResult::Prob(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::exponential_cdf ( double  x,
double  lambda,
double  x0 = 0 
)

Cumulative distribution function of the exponential distribution (lower tail).

\[ D(x) = \int_{-\infty}^{x} \lambda e^{-\lambda x'} dx' \]

For detailed description see Mathworld.

Definition at line 93 of file ProbFuncMathCore.cxx.

References ROOT::Math::expm1().

Referenced by ROOT::Math::GoFTest::ExponentialCDF(), G__G__MathCore_170_0_36(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::exponential_cdf_c ( double  x,
double  lambda,
double  x0 = 0 
)

Complement of the cumulative distribution function of the exponential distribution (upper tail).

\[ D(x) = \int_{x}^{+\infty} \lambda e^{-\lambda x'} dx' \]

For detailed description see Mathworld.

Definition at line 77 of file ProbFuncMathCore.cxx.

References exp().

Referenced by G__G__MathCore_170_0_35(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::fdistribution_cdf ( double  x,
double  n,
double  m,
double  x0 = 0 
)

Cumulative distribution function of the F-distribution (lower tail).

\[ D_{n,m}(x) = \int_{-\infty}^{x} \frac{\Gamma(\frac{n+m}{2})}{\Gamma(\frac{n}{2}) \Gamma(\frac{m}{2})} n^{n/2} m^{m/2} x'^{n/2 -1} (m+nx')^{-(n+m)/2} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete beta function, ROOT::Math::inc_beta, from Cephes

Definition at line 123 of file ProbFuncMathCore.cxx.

References ROOT::Math::fdistribution_cdf_c(), and ROOT::Math::inc_beta().

Referenced by TMath::FDistI(), ROOT::Math::fdistribution_cdf_c(), G__G__MathCore_170_0_38(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::fdistribution_cdf_c ( double  x,
double  n,
double  m,
double  x0 = 0 
)

Complement of the cumulative distribution function of the F-distribution (upper tail).

\[ D_{n,m}(x) = \int_{x}^{+\infty} \frac{\Gamma(\frac{n+m}{2})}{\Gamma(\frac{n}{2}) \Gamma(\frac{m}{2})} n^{n/2} m^{m/2} x'^{n/2 -1} (m+nx')^{-(n+m)/2} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete beta function, ROOT::Math::inc_beta, from Cephes

Definition at line 108 of file ProbFuncMathCore.cxx.

References ROOT::Math::fdistribution_cdf(), and ROOT::Math::inc_beta().

Referenced by ROOT::Math::fdistribution_cdf(), G__G__MathCore_170_0_37(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::gamma_cdf ( double  x,
double  alpha,
double  theta,
double  x0 = 0 
)

Cumulative distribution function of the gamma distribution (lower tail).

\[ D(x) = \int_{-\infty}^{x} {1 \over \Gamma(\alpha) \theta^{\alpha}} x'^{\alpha-1} e^{-x'/\theta} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete gamma function, ROOT::Math::inc_gamma, from Cephes

Definition at line 145 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_gamma().

Referenced by RooGamma::analyticalIntegral(), G__G__MathCore_170_0_40(), G__setup_memfuncROOTcLcLMath(), myfunc(), ROOT::Math::poisson_cdf_c(), RooMathCoreReg::RooMathCoreReg(), and testGammaFunction().

double ROOT::Math::gamma_cdf_c ( double  x,
double  alpha,
double  theta,
double  x0 = 0 
)

Complement of the cumulative distribution function of the gamma distribution (upper tail).

\[ D(x) = \int_{x}^{+\infty} {1 \over \Gamma(\alpha) \theta^{\alpha}} x'^{\alpha-1} e^{-x'/\theta} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete gamma function, ROOT::Math::inc_gamma, from Cephes

Definition at line 137 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_gamma_c().

Referenced by G__G__MathCore_170_0_39(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::poisson_cdf(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::landau_cdf ( double  x,
double  xi = 1,
double  x0 = 0 
)

Cumulative distribution function of the Landau distribution (lower tail).

\[ D(x) = \int_{-\infty}^{x} p(x) dx \]

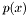where $p(x)$ is the Landau probability density function :

\[ p(x) = \frac{1}{\xi} \phi (\lambda) \]

with

\[ \phi(\lambda) = \frac{1}{2 \pi i}\int_{c-i\infty}^{c+i\infty} e^{\lambda s + s \log{s}} ds\]

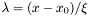with $\lambda = (x-x_0)/\xi$. For a detailed description see K.S. Kölbig and B. Schorr, A program package for the Landau distribution, Computer Phys. Comm. 31 (1984) 97-111 [Erratum-ibid. 178 (2008) 972]. The same algorithms as in CERNLIB (DISLAN) is used.

Parameters:
x The argument 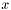$x$
xi The width parameter 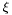$\xi$
x0 The location parameter 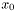$x_0$

Definition at line 302 of file ProbFuncMathCore.cxx.

References exp(), log(), p1(), p2(), p3(), p4(), sqrt(), and u.

Referenced by G__G__MathCore_170_0_41(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::landau_cdf_c(), TMath::LandauI(), RooMathCoreReg::RooMathCoreReg(), and ROOT::Math::VavilovFast::SetKappaBeta2().

double ROOT::Math::landau_cdf_c ( double  x,
double  xi = 1,
double  x0 = 0 
) [inline]

Complement of the distribution function of the Landau distribution (upper tail).

\[ D(x) = \int_{x}^{+\infty} p(x) dx \]

where p(x) is the Landau probability density function. It is implemented simply as 1. - landau_cdf

Parameters:
x The argument 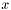$x$
xi The width parameter 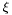$\xi$
x0 The location parameter 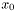$x_0$

Definition at line 370 of file ProbFuncMathCore.h.

References ROOT::Math::landau_cdf(), and x0.

Referenced by G__G__MathCore_170_0_42(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::lognormal_cdf ( double  x,
double  m,
double  s,
double  x0 = 0 
)

Cumulative distribution function of the lognormal distribution (lower tail).

\[ D(x) = \int_{-\infty}^{x} {1 \over x' \sqrt{2 \pi s^2} } e^{-(\ln{x'} - m)^2/2 s^2} dx' \]

For detailed description see Mathworld.

Definition at line 166 of file ProbFuncMathCore.cxx.

References ROOT::Math::erf(), ROOT::Math::erfc(), ROOT::Math::kSqrt2, and log().

Referenced by G__G__MathCore_170_0_44(), G__setup_memfuncROOTcLcLMath(), goftest(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::lognormal_cdf_c ( double  x,
double  m,
double  s,
double  x0 = 0 
)

Complement of the cumulative distribution function of the lognormal distribution (upper tail).

\[ D(x) = \int_{x}^{+\infty} {1 \over x' \sqrt{2 \pi s^2} } e^{-(\ln{x'} - m)^2/2 s^2} dx' \]

For detailed description see Mathworld.

Definition at line 154 of file ProbFuncMathCore.cxx.

References ROOT::Math::erf(), ROOT::Math::erfc(), ROOT::Math::kSqrt2, and log().

Referenced by G__G__MathCore_170_0_43(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::negative_binomial_cdf ( unsigned int  k,
double  p,
double  n 
)

Cumulative distribution function of the Negative Binomial distribution Lower tail of the integral of the negative_binomial_pdf

Definition at line 282 of file ProbFuncMathCore.cxx.

References ROOT::Math::beta_cdf().

Referenced by G__G__MathCore_170_0_58(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::negative_binomial_cdf_c ( unsigned int  k,
double  p,
double  n 
)

Complement of the cumulative distribution function of the Negative Binomial distribution. Upper tail of the integral of the negative_binomial_pdf

Definition at line 291 of file ProbFuncMathCore.cxx.

References ROOT::Math::beta_cdf_c().

Referenced by G__G__MathCore_170_0_57(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::normal_cdf ( double  x,
double  sigma = 1,
double  x0 = 0 
)

Cumulative distribution function of the normal (Gaussian) distribution (lower tail).

\[ D(x) = \int_{-\infty}^{x} {1 \over \sqrt{2 \pi \sigma^2}} e^{-x'^2 / 2\sigma^2} dx' \]

For detailed description see Mathworld.

Definition at line 191 of file ProbFuncMathCore.cxx.

References ROOT::Math::erf(), ROOT::Math::erfc(), and ROOT::Math::kSqrt2.

Referenced by cdf(), cdf_trunc(), G__G__MathCore_170_0_47(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::gaussian_cdf(), ROOT::Math::GoFTest::GaussianCDF(), RooMathCoreReg::RooMathCoreReg(), testMultinomial(), and unuranSimple().

double ROOT::Math::normal_cdf_c ( double  x,
double  sigma = 1,
double  x0 = 0 
)

Complement of the cumulative distribution function of the normal (Gaussian) distribution (upper tail).

\[ D(x) = \int_{x}^{+\infty} {1 \over \sqrt{2 \pi \sigma^2}} e^{-x'^2 / 2\sigma^2} dx' \]

For detailed description see Mathworld.

Definition at line 178 of file ProbFuncMathCore.cxx.

References ROOT::Math::erf(), ROOT::Math::erfc(), and ROOT::Math::kSqrt2.

Referenced by G__G__MathCore_170_0_45(), G__setup_memfuncROOTcLcLMath(), ROOT::Math::gaussian_cdf_c(), RooMathCoreReg::RooMathCoreReg(), and RooStats::SignificanceToPValue().

double ROOT::Math::poisson_cdf ( unsigned int  n,
double  mu 
)

Cumulative distribution function of the Poisson distribution Lower tail of the integral of the poisson_pdf

Definition at line 255 of file ProbFuncMathCore.cxx.

References a, double, and ROOT::Math::gamma_cdf_c().

Referenced by RooPoisson::analyticalIntegral(), G__G__MathCore_170_0_54(), G__setup_memfuncROOTcLcLMath(), RooMathCoreReg::RooMathCoreReg(), and testPoissonCdf().

double ROOT::Math::poisson_cdf_c ( unsigned int  n,
double  mu 
)

discrete distributions

Complement of the cumulative distribution function of the Poisson distribution. Upper tail of the integral of the poisson_pdf

Definition at line 248 of file ProbFuncMathCore.cxx.

References a, double, and ROOT::Math::gamma_cdf().

Referenced by G__G__MathCore_170_0_53(), G__setup_memfuncROOTcLcLMath(), RooMathCoreReg::RooMathCoreReg(), and testPoissonCdf().

double ROOT::Math::tdistribution_cdf ( double  x,
double  r,
double  x0 = 0 
)

Cumulative distribution function of Student's t-distribution (lower tail).

\[ D_{r}(x) = \int_{-\infty}^{x} \frac{\Gamma(\frac{r+1}{2})}{\sqrt{r \pi}\Gamma(\frac{r}{2})} \left( 1+\frac{x'^2}{r}\right)^{-(r+1)/2} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete beta function, ROOT::Math::inc_beta, from Cephes

Definition at line 213 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_beta(), p, and RootCsg::sign().

Referenced by G__G__MathCore_170_0_50(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::tdistribution_cdf_c ( double  x,
double  r,
double  x0 = 0 
)

Complement of the cumulative distribution function of Student's t-distribution (upper tail).

\[ D_{r}(x) = \int_{x}^{+\infty} \frac{\Gamma(\frac{r+1}{2})}{\sqrt{r \pi}\Gamma(\frac{r}{2})} \left( 1+\frac{x'^2}{r}\right)^{-(r+1)/2} dx' \]

For detailed description see Mathworld. It is implemented using the incomplete beta function, ROOT::Math::inc_beta, from Cephes

Definition at line 203 of file ProbFuncMathCore.cxx.

References ROOT::Math::inc_beta(), p, and RootCsg::sign().

Referenced by G__G__MathCore_170_0_49(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::uniform_cdf ( double  x,
double  a,
double  b,
double  x0 = 0 
)

Cumulative distribution function of the uniform (flat) distribution (lower tail).

\[ D(x) = \int_{-\infty}^{x} {1 \over (b-a)} dx' \]

For detailed description see Mathworld.

Definition at line 235 of file ProbFuncMathCore.cxx.

Referenced by G__G__MathCore_170_0_52(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::uniform_cdf_c ( double  x,
double  a,
double  b,
double  x0 = 0 
)

Complement of the cumulative distribution function of the uniform (flat) distribution (upper tail).

\[ D(x) = \int_{x}^{+\infty} {1 \over (b-a)} dx' \]

For detailed description see Mathworld.

Definition at line 222 of file ProbFuncMathCore.cxx.

Referenced by G__G__MathCore_170_0_51(), G__setup_memfuncROOTcLcLMath(), and RooMathCoreReg::RooMathCoreReg().

double ROOT::Math::vavilov_accurate_cdf ( double  x,
double  kappa,
double  beta2 
)

The Vavilov cummulative probability density function

Parameters:
x The Landau parameter 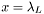$x = \lambda_L$
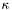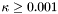kappa The parameter $\kappa$, which must be in the range $\kappa \ge 0.001 $
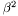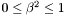beta2 The parameter $\beta^2$, which must be in the range $0 \le \beta^2 \le 1 $

Definition at line 472 of file VavilovAccurate.cxx.

References ROOT::Math::VavilovAccurate::GetInstance(), and vavilov().

Referenced by G__G__MathMore_99_0_38(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::vavilov_accurate_cdf_c ( double  x,
double  kappa,
double  beta2 
)

The Vavilov complementary cummulative probability density function

Parameters:
x The Landau parameter 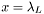$x = \lambda_L$
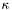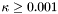kappa The parameter $\kappa$, which must be in the range $\kappa \ge 0.001 $
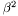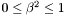beta2 The parameter $\beta^2$, which must be in the range $0 \le \beta^2 \le 1 $

Definition at line 467 of file VavilovAccurate.cxx.

References ROOT::Math::VavilovAccurate::GetInstance(), and vavilov().

Referenced by G__G__MathMore_99_0_39(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::vavilov_fast_cdf ( double  x,
double  kappa,
double  beta2 
)

The Vavilov cummulative probability density function

Parameters:
x The Landau parameter 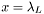$x = \lambda_L$
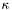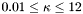kappa The parameter $\kappa$, which must be in the range $0.01 \le \kappa \le 12 $
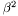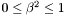beta2 The parameter $\beta^2$, which must be in the range $0 \le \beta^2 \le 1 $

Definition at line 583 of file VavilovFast.cxx.

References ROOT::Math::VavilovFast::GetInstance(), and vavilov().

Referenced by G__G__MathMore_99_0_43(), and G__setup_memfuncROOTcLcLMath().

double ROOT::Math::vavilov_fast_cdf_c ( double  x,
double  kappa,
double  beta2 
)

The Vavilov complementary cummulative probability density function

Parameters:
x The Landau parameter 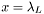$x = \lambda_L$
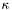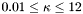kappa The parameter $\kappa$, which must be in the range $0.01 \le \kappa \le 12 $
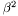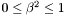beta2 The parameter $\beta^2$, which must be in the range $0 \le \beta^2 \le 1 $

Definition at line 588 of file VavilovFast.cxx.

References ROOT::Math::VavilovFast::GetInstance(), and vavilov().

Referenced by G__G__MathMore_99_0_44(), and G__setup_memfuncROOTcLcLMath().

Generated on Tue Jul 5 16:09:42 2011 for ROOT_528-00b_version by  doxygen 1.5.1